1．顺序查找法以及平均查找长度（ASL）的计算；
2．折半查找法以及平均查找长度（ASL）的计算，包括查找过程对应的“判定树”的构造；
3．散列（Hash）表的构造、散列函数的构造，散列冲突的基本概念、处理散列冲突的基本方法以及散列表的查找和平均查找长度的计算。

1. 名词解释

• 平均查找长度 ASL：确定一个记录在文件中的位置所需要进⾏的关键字值的⽐较次数的期望值（平均值）。
  对于具有 n 个记录的文件，查找成功的平均查找长度为： $ASL = \sum_{i=1}^n {p_ic_i}$。
  其中，$p_i$ 为查找第 i 个记录的概率，$c_i$ 为查找第 i 个记录所进行过的关键字的比较次数。

2．顺序查找法以及平均查找长度（ASL）的计算；

2.1 查找思想：

1. 从文件的第一个记录开始，将用户给出的关键字值与当前被查找记录的关键字值进行比较。
2. 若匹配，则查找成功，给出被查到的记录在文件中的位置，查找结束。
3. 若所有 n 个记录的关键字值都已比较，不存在与用户要查的关键字值匹配的记录，则查找失败，给出信息 0。

2.2 算法实现

int SEQ_SEARCH(int key[], int n, int k) {
    for (int i = 1; i <= n; i++) {
        if (key[i] == k) {
            return i; /* 查找成功 */
        }
    }
    return 0; /* 查找失败 */
}

• 算法时间复杂度：$O(n)$。

2.3 平均查找长度（ASL）：

$ASL = \sum_{i=1}^n {p_ic_i} = {1 \over n} \sum_{i=1}^n i = {n+1 \over 2}$。

3．折半查找法以及平均查找长度（ASL）的计算，包括查找过程对应的“判定树”的构造；

3.1 查找思想

1. 将要查找的关键字值与当前查找范围内位置居中的记录的关键字的值进行比较。
2. 若匹配，则查找成功，给出被查到记录在文件中的位置，查找结束。
3. 若要查找的关键字值小于位置居中的记录的关键字值，则到当前查找范围的前半部分重复上述查找过程。
4. 否则，到当前查找范围的后半部分重复上述查找过程，直到查找成功或者失败。
5. 若查找失败，则给出信息0。

3.2 算法实现

/* key[1:n] 存放已经排好序的关键字数组 */
int BIN_SEARCH(int key[], int n, int k) {
    int low = 1, high = n, mid;
    while (low <= high) {
        mid = (low+high)/2;
        if (key[mid] == k) {
            return mid; /* 查找成功 */
        }
        if (k > key[mid]) {
            low = mid+1; /* 查找后半部分 */
        } else {
            high = mid-1; /* 查找前半部分 */
        }
    }
    return 0; /* 查找失败 */
}

• 算法时间复杂度：$O(log_2 n)$。

3.3 判定树

若把当前查找范围内居中的记录的位置作为根结点，前半部分与后半部分的记录的位置分别构成根结点的左子树与右子树，则由此可得到一棵称为「判定树」的二叉树，利用它来描述折半查找的过程。

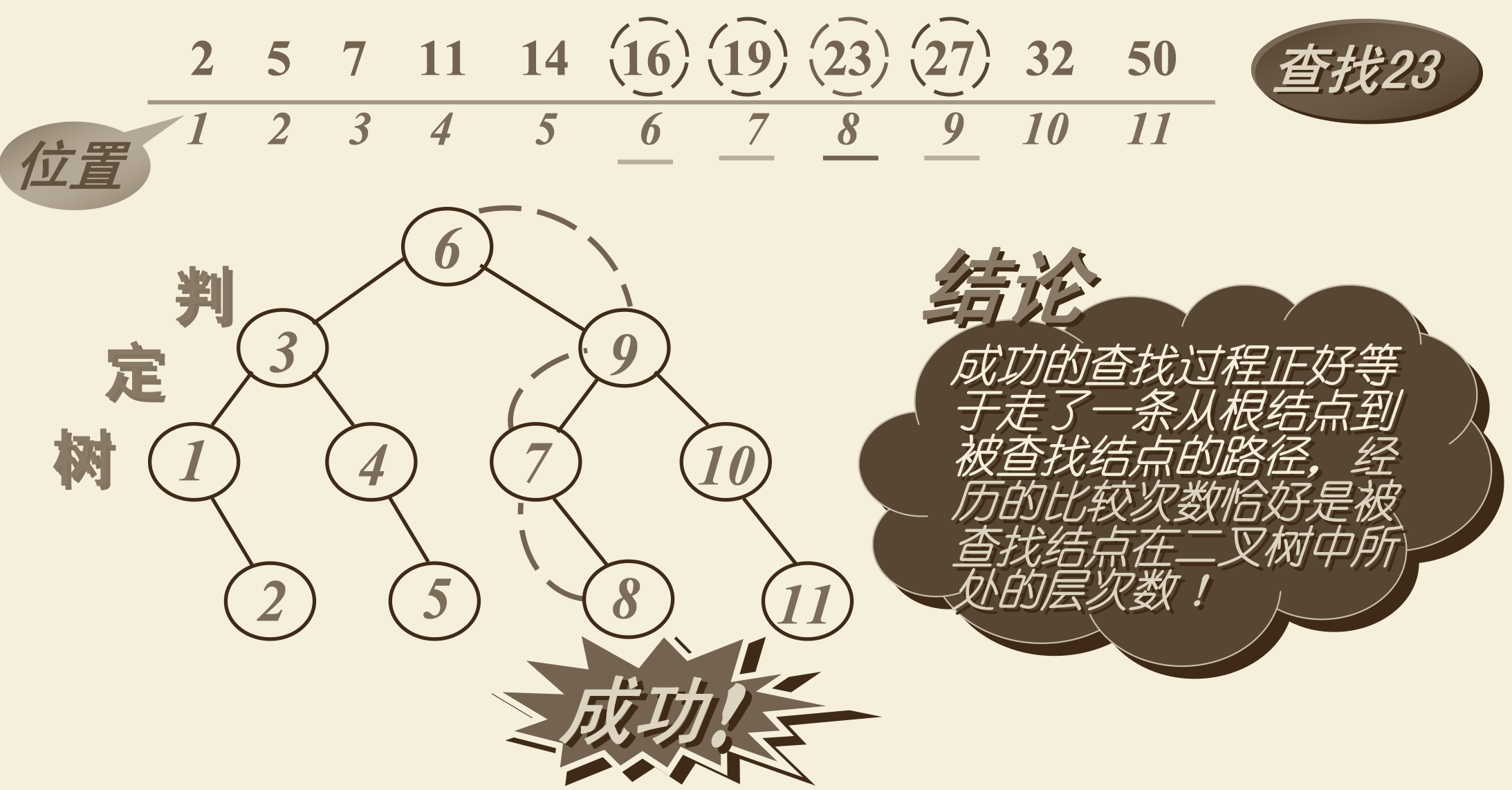
3.4 平均查找长度（ASL）：

为了简化讨论，则吧判定树近似的看为一棵满二叉树，根据二叉树的性质，它有最大结点数 $n = 2^h - 1$，深度 $h = log_2 (n+1)$。二叉树中第 j 层的结点数为 $2^{j-1}$，若对于排序连续顺序文件，假定每个元素的查找概率相等，有 $p_i = {1 \over n}$，则有：

$ASL = \sum_{i=1}^n {p_ic_i} = {1 \over n} \sum_{j=1}^h j*2^{j-1} = {n+1 \over n} log_2 (n+1) -1$。

当 n 较大时，$ASL = log_2 (n+1) - 1$。

3.5 二分查找优缺点：

优点：

• 查找原理和过程简单，易于理解。
• 查找的时间效率较高。

缺点：

• 要求文件的记录按照关键字值有序排列。
• 为保持文件的记录按照关键字值有序排列， 在文件中插入和删除记录时需要移动大量的其它记录。

4．散列（Hash）表的构造、散列函数的构造，散列冲突的基本概念、处理散列冲突的基本方法以及散列表的查找和平均查找长度的计算。

4.1 定义解释

1. 散列方法：
   在记录的存储位置与该记录的关键字值之间建立一种确定的对应关系，使得每个记录的关键字值与结构中一个唯一的存储位置相对应。这样查找一个记录，只需要根据这个对应关系就可以查找到索要找的记录。若结构中存在关键字与给定记录相等的记录，则必然在此位置上，不需要进行关键字的比较便可以直接取得所查的记录。这种存储方法称为 散列（hash）方法。
2. 散列函数：
   记录的存储位置 A 与 记录关键字值 k 的函数，称为散列函数、哈希函数或杂凑函数 $H(k)$。函数值 A 为 k 对应的记录在文件中的位置。即：$A = H(k)$。
3. 散列冲突：
   对于不同的关键字 $k_i$ 与 $k_j$，经过散列得到相同的散列地址，即有 $H(k_i) = H(k_j)$。这种现象称为散列冲突。
4. 散列文件：
   根据构造的散列函数与处理冲突的方法将一组关键字映射到一个有限的连续地址集合上，并以关键字在该集合中的“象”作为记录的存储位置，按照这种方法组织起来文件称为散列文件，或称哈希文件，或称杂凑文件；建立文件的过程称为哈希造表或者散列， 得到的存储位置称为散列地址或者杂凑地址。

4.2 散列函数的构造

4.2.1 构造原则

1. 散列函数的定义域必须包括将要存储的全部关键码；若散列表允许有 m 个位置时，则函数的值域为 [0：m–1]（地址空间）。
2. 利用散列函数计算出来的地址应能尽可能均匀分布在整个地址空间中。
3. 散列函数应该尽可能简单， 应该在较短的时间内计算出结果。

4.2.2 构造步骤

1. 确定散列表的地址空间（地址范围），即确定散列函数值域；
2. 构造合适的散列函数，该散列函数要保证所有可能元素的散列函数值均在指定的值域内，并使得冲突发生的可能性尽可能小；
3. 选择处理冲突的有效方法。

4.2.3 构造方法

4.2.3.1 直接定址法

• 取关键字值的某个线性函数作为散列函数，即 $H(k) = ak + b$。
• 适合于关键字分布基本连续，或者关键字值有一定规律的情况。
• 如果关键字值分布不连续，空号较多，这种方法将会造成存储空间的浪费。另外，当关键字表示的范围很大，且无规律时，也不适合采用这种方法。
• 例如：建立某个地区一个从 1 岁到 100 岁的人口数字统计表。设给定表的空间范围为 [1001，1100]，以年龄为关键字，则可以构造散列函数为 $H(k) = k + 1000$。将关键字代入该散列函数，可以得到各个年龄以及相应人口数的存放位置，并建立如下图所示的散列表作为人口统计表。
  

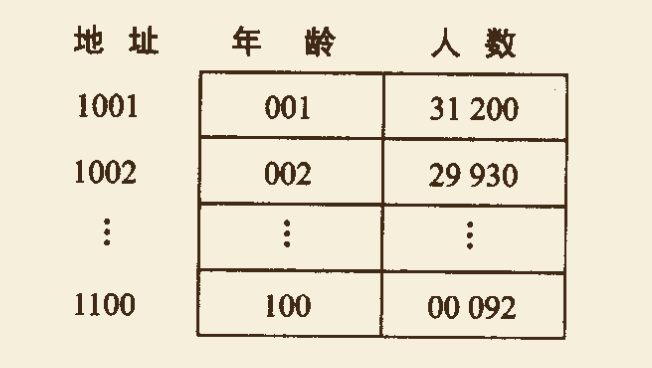
4.2.3.2 数字分析法

• 当关键字值的位数大于散列地址码的位数时，对关键字值的各位数字进行分析，从中取出与散列地址位数相同的位。
• 假设关键字值是以 r 为基的数，并且可能值事先已知，则从中人已去除相当多的关键字值进行分析，舍去数字分布不均匀的那些位，而将其中位置分布比较均匀的若干位组成散列地址。
• 数字分析法比较适用于当所有关键字可能出现的值都已知的情况。但在许多情况下，构造散列函数的时候并不一定知道关键字的全部情况，这时采用数字分析法构造散列函数就不合适了。
• 例如：一个散列表的地址范围为 [000，999]，关键字值均为 8 位十进制数，从中抽取 7 个元素如下图：
  
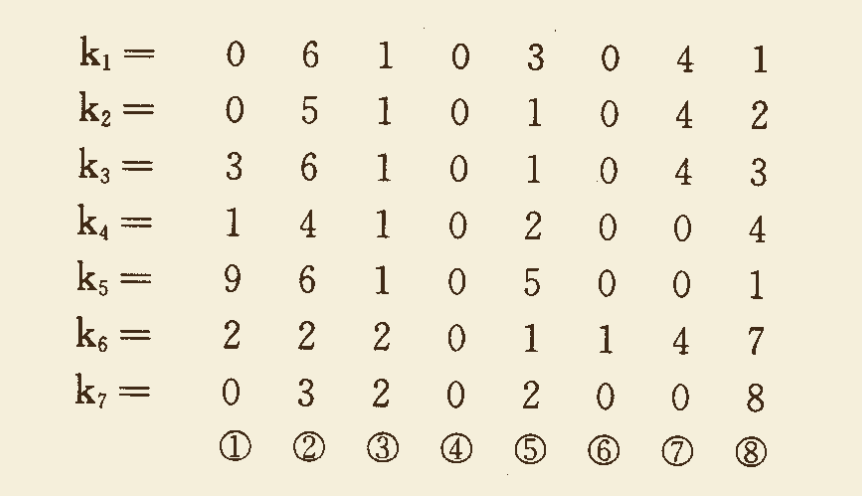
  分析其中每一位的位值分布情况发现，第 8 位（最右边一位）出现了 6 种不同数字（1、2、3、4、7、8），第 1 位出现了 5 种不同数字（0、1、2、3、9），第 2 位出现了 5 种不同数字（2、3、4、5、6），其他各位出现的数字种类不较少，为此可以取关键字值第 1位、第 2 位、第 8 位的位值组成散列函数值，得：
  $H(k_1) = 061 \quad H(k_2) = 052 \quad H(k_3) = 363 \quad H(k_4) = 144 \ H(k_5) = 961 \quad H(k_6) = 227 \quad H(k_7) = 038$

4.2.3.3 平方取中法

• 先计算关键字值的平方，然后又目的地选取中间的若干位作为散列地址。具体取哪几位以及取哪几位要根据实际需要来确定。由于一个数经过平方之后的中间几位数字与数的每一位都有关，从而不难知道，采用平方取中法得到的散列地址与关键字的每一位都有关，因而使得散列地址具有很好的分散性，得到的散列地址也具有较好的随机性。
• 平方取中法适用于关键字值中的每一位取值都不够分散，或者相对比较分散的位数小于散列地址所需要的位数的情况。
• 例如：若设散列的地址范围为 [000，999]，k = 4731，则 $k^2 = 22382361$，取中间第 3 位至第 5 位作为相应散列地址，则有 $H(k) = 382$。

4.2.3.4 叠加法

• 把关键字值分割成位数相同的几个部分（最后一个部分的位数如不够，不足位左边可以空缺），然后把这几个部分的叠加和（舍去进位）作为散列地址。
• 在位数很多且位值分布比较均匀时，可以考虑采用这种方法。具体有 移位叠加法 和 折叠叠加法 两种叠加法。
• 位移叠加法：把分割后的每一部分进行右对齐，然后相加。
  • 例如：散列地址范围为 [000，999]，某关键字值为 k = 72320324112。可按 3 位一段进行划分，位移叠加如下：
    
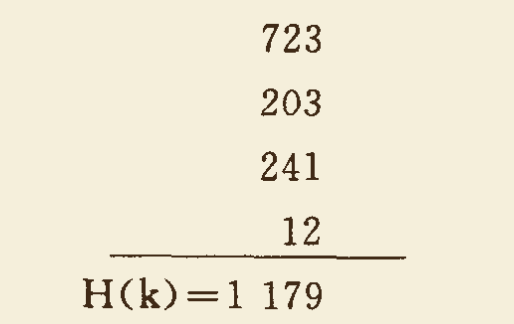
    舍弃进位 1，将 179 作为 k 的散列地址。
• 折叠叠加法：把分割后的每一部分进行来回折叠相加。
  • 例如：散列地址范围为 [000，999]，某关键字值为 k = 72320324112。可按 3 位一段进行划分，位移叠加如下：
    
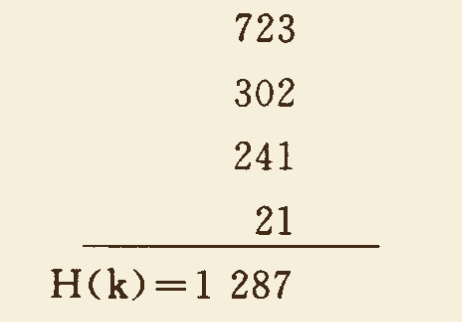
    舍弃进位 1，将 287 作为 k 的散列地址。

4.2.3.5 基数转换法

• 设关键字值原来是十进制数，人为地当做 q 进制数，再转成十进制数后作为散列地址。
• 例如： $k = 4731_{10}，q = 13$，则
  $H(k) = 4 \times 13^3 + 7 \times 13^2 + 3 \times 13^1 + 1 \times 13^0 = 10 011_{10}$。

4.2.3.6 除留余数法

• 设散列范围的长度为 m，该方法是将关键字值 k 除以某数 $p (p \le m)$ 以后所得到的余数作为散列地址。$H(k) = k \ MOD\ p$，其中，若 m 为地址范围大小（或称表长）， 则 p 可为小于等于 m 的素数。
• 除留余数法的地址计算比较简单，使用范围也比较广，是一种最常见的方法。
• 例如：若表长 m = 128，可选 p = 127。当 k = 4731 时，则有 $H(k) = 4731 \ MOD \ 127 = 32$。

4.2.3.7 随机数法

• 选择一个随机函数，取关键字的随机函数值为它的散列地址。即 $H(k) = random(k)$，其中 $random(k)$ 为随机函数。
• 随机数法适用于关键字长度不等的情况。

4.2.4 冲突处理方法

所谓处理冲突，是在发生冲突时，为冲突的元素找到另一个散列地址以存放该元素。如果找到的地址仍然发生冲突，则继续为发生冲突的这个元素寻找另一个地址，直到不再发生冲突。

4.2.4.1 开放地址法

• 所谓开放地址法是在散列表中的“空”地址向处理冲突开放。即当散列表未满时，处理冲突需要的“下一个” 地址在该散列表中解决。

• $D_i = ( H(k) + d_i ) \ MOD \ m \quad i = 1, 2, 3, …$

• 其中，$H(k)$ 为散列函数，m 为散列表长，$d_i$ 为地址增量，有以下几种方法：

  1. $d_i =1，2，3，…，m–1$，称为线性再散列
  2. $d_i =1^2，2^2，…，(\lfloor m/2 \rfloor)^2$，称为二次再散列
  3. $d_i = 伪随机数序列$，称为伪随机再散列

• 这里，对散列表长 m 取模的目的主要是为了使得到的 "下一个" 地址一定落在散列表内。

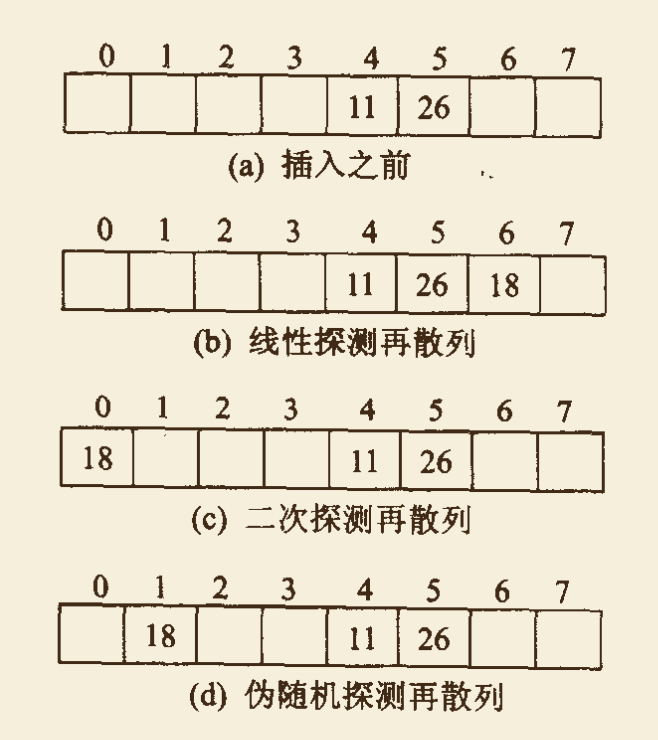
• 例如：散列函数为 $H(k) = k \ MOD \ 7$，散列表长 m = 8。假设表中已存入元素 11 和 26。如下图（a）。若要再存入元素 18，由散列函数计算散列地址为 4，则在此位置发生冲突。

  • 若采用线性在散列处理冲突，则在 4 的基础上增加一个地址增量 1，得到地址 $D_1 = (4 + 1) \ MOD \ 8 = 5$，在地址 $D_1$ 处仍出现冲突，若在 4 的基础上增加一个地址增量 2，得地址 $D_2 = 6$，该地址处不发生冲突，可存入元素 18。此时，散列表的状态如下图（b）所示。
  • 若采用二次再散列处理冲突，则在 4 的基础上增加地址增量 $1^2$，得到地址 $D_1 = (4 + 1) \ MOD \ 8 = 5$，在地址 $D_1$ 处仍然发生冲突；然后再在 4 的基础上增加地址增量 $2^2$，得到地址 $D_2 = (4+4) \ MOD \ 8 = 0$，此处没有发生冲突，元素 18 存入位置 0 中，此时，散列表的状态如下图（c）所示。
  • 若采用伪随机再散列处理冲突，假设伪随机数为 5，则得到地址 $D_1 = (4+5) \ MOD \ 8 = 1$，此处没有发生冲突，元素 18 应存入位置 1 中，此时，散列表的状态如下图（d）所示。
    

4.2.4.2 再散列法

在发生冲突时，用不同的散列函数再求得新的散列地址，直到不发生冲突时为止，即
$D_i = H_i(k) \quad i = 1，2，…，n$。其中，$H_i(k)$ 表示第 i 个散列函数。

采用这种方法一般情况下不易发生冲突，但增加了计算时间的开销，而且要求事先构造多个散列函数，这种方法在实际应用过程中有较大的局限性。

4.2.4.3 链地址法

1. 将哈希文件分为基本区与溢出区两个部分，没有发生冲突的记录放在基本区，当发生冲突时，把具有相同散列地址的记录存放在溢出区，并把具有相同地址的记录采用 一个线性链表链接起来。
   
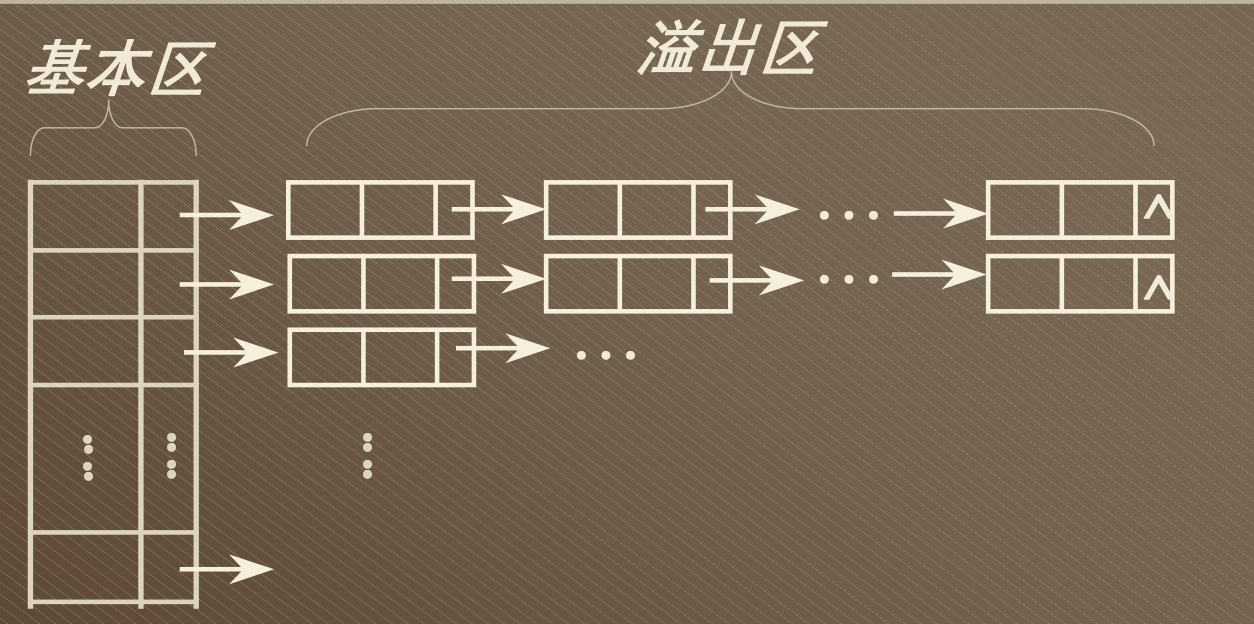
2. 不分基本区与溢出区。将所有散列地址相同的记录链接成一个线性链表。若散列范围为[ 0: m-1]，则定义一个指针数组 bucket[ 0 : m-1 ] 分别存放 m 个链表的头指针。
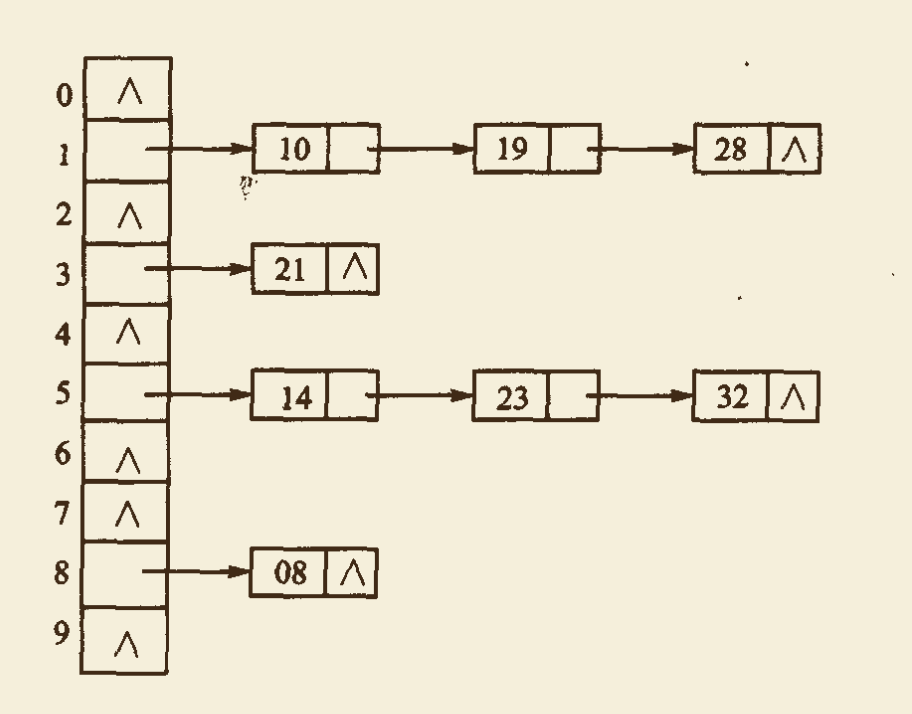
   • 例如：m = 10，散列地址范围为 [0，9]，散列函数为 H(k) = k MOD 9。散列表中已经先后存入的元素为 08，10，14，19，21，23，28，32。
     

4.3 散列表的查找

在散列文件中查找记录的过程与建立散列文件的过程相似。通常按照下列步骤查找一个记录。

1. 根据给定的关键字值 k，计算出散列地址 H(k)。
2. 若该地址为空，则表中没有要查找的记录，查找结束；否则进行步骤 3。
3. 若该地址中的关键字值与 k 值相等，则查找成功，结束查找；否则进行步骤 4。
4. 根据处理冲突的方法求得下一个散列地址，转执行步骤 2。

4.4 散列法的平均查找长度

构造散列函数时，为了使得范围广泛的关键字域映射到一组指定的连续空间中个，放弃了一一对应的映射关系，引入了冲突的概念，使得散列文件的建立和查找过程仍然是一个与关键字值比较的过程，从而增加了查找时间。
而发生冲突的次数与散列表的填满程度直接相关，即负载因子越大，表越满，冲突的可能性就越大，查找也就越满。因此，散列表查找成功的平均查找长度与负载因子 α 有关。

1. 对于采用线性探测再散列处理冲突的散列表，其查找成功的平均查找长度为：
   $S_{nl} \approx {1 \over 2} (1 + {1 \over 1 - \alpha})$
2. 对于采用伪随机探测再散列和二次探测再散列处理冲突时，查找成功的平均查找长度为：
   $S_{nr} \approx -{1 \over \alpha} ln(1 - \alpha)$
3. 若采用链地址法处理冲突，则查找成功时的平均查找长度为：
   $S_{nc} \approx 1 + {\alpha \over 2}$

由于查找不成功所用的比较次数也与给定值有关，因而可以类似地定义查找不成功的平均查找长度，即查找不成功的平均查找长度为需要与给定值进行比较的关键字个数的期望值。

1. 对于采用线性探测再散列处理冲突的散列表，其查找失败的平均查找长度为：
   $U_{nl} \approx {1 \over 2}[1 + {1 \over (1 - \alpha)^2}]$
2. 对于采用伪随机探测再散列和二次探测再散列处理冲突时，查找失败的平均查找长度为：
   $U_{nr} \approx {1 \over 1 - \alpha}$
3. 若采用链地址法处理冲突，则查找失败时的平均查找长度为：
   $U_{nc} \approx \alpha + e^{-\alpha}$

散列法的平均长度是负载因子 $\alpha$ 的函数，与散列表的长度 m 无关。