数据结构（考纲总结）：五、树与二叉树

2018-08-27

9.466k 字 | 32 分钟

1．树与二叉树的基本概念，基本特征、名词术语；
2．完全二叉树与满二叉树的基本概念，二叉树的基本性质及其应用；
3．二叉树的顺序存储结构与二叉链表存储结的基本原理；
4．二叉树的前序遍历、中序遍历、后序遍历和按层次遍历，重点是二叉树在以二叉链表作为存储结构基础上各种遍历算法（包括非递归算法）的设计与应用；
5．二叉排序树的基本概念、建立（插入）、查找以及平均查找长度ASL的计算。

1．树与二叉树的基本概念，基本特征、名词术语；

1.1 树的定义

树是由 $n \ge 0$ 个结点组成的有穷集合（不妨用符号D表示）以及结点之间关系组成的集合构成的结构。当 $n=0$ 时，称该树为空树；
在任何⼀棵⾮空的树中，有⼀个特殊的结点 $t \in D$，称之为该树的根结点；其余结点 $D–{t}$ 被分割成 $m > 0$ 个不相交的子集$ D_1,D_2 , … ,D_m$ ,其中每一个子集 $D_i$ 又为一棵树，分别称之为 t 的子树。

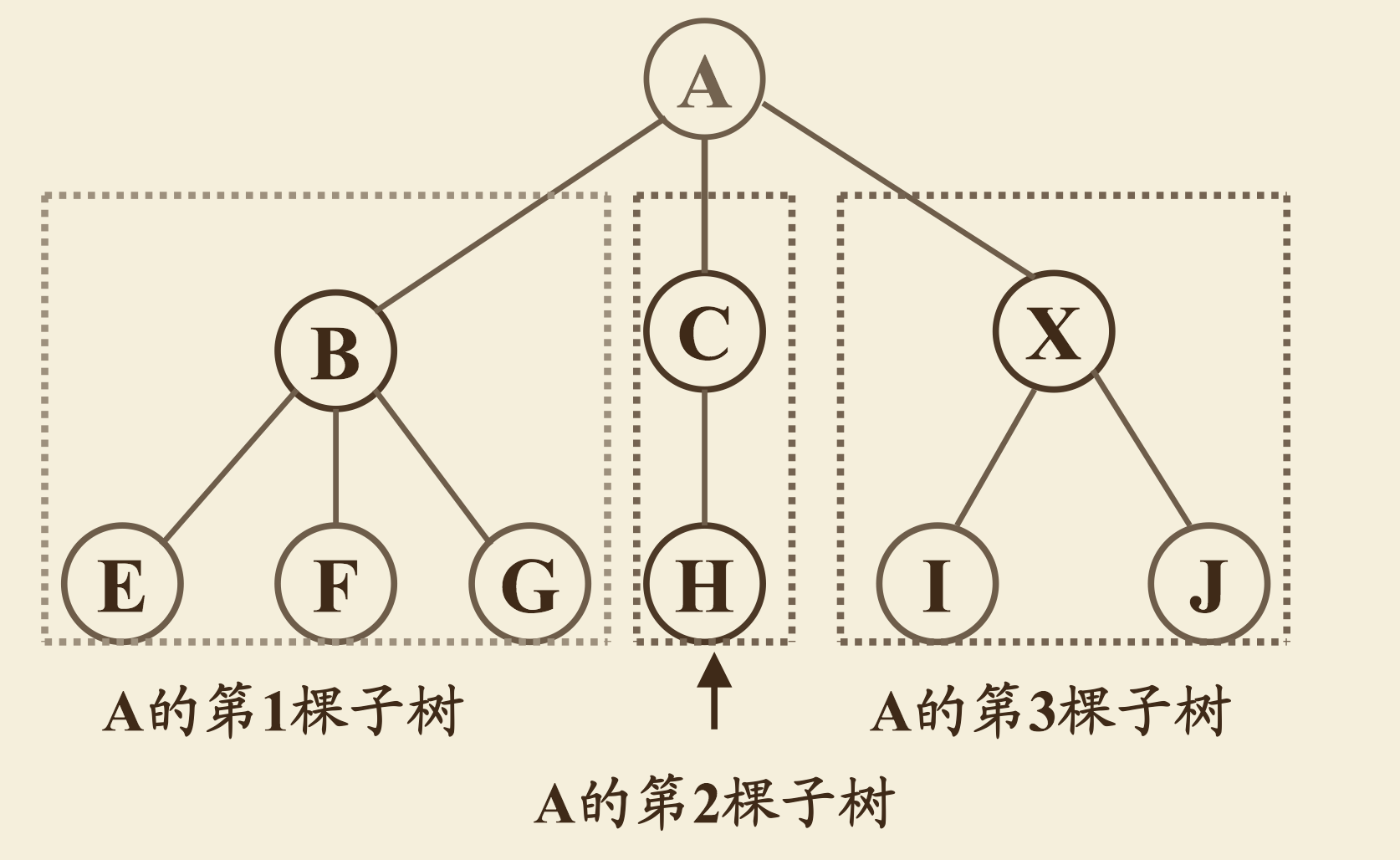
1.2 树的基本特征

有且仅有一个结点没有前驱结点,该结点为树的根结点；
除了根结点外,每个结点有且仅有一个直接前驱结点；
包括根结点在内，每个结点可以有多个后继结点。

1.3 树的逻辑表示方法

文氏图表示法
凹入表示法
嵌套括号表示法（广义表表示法）
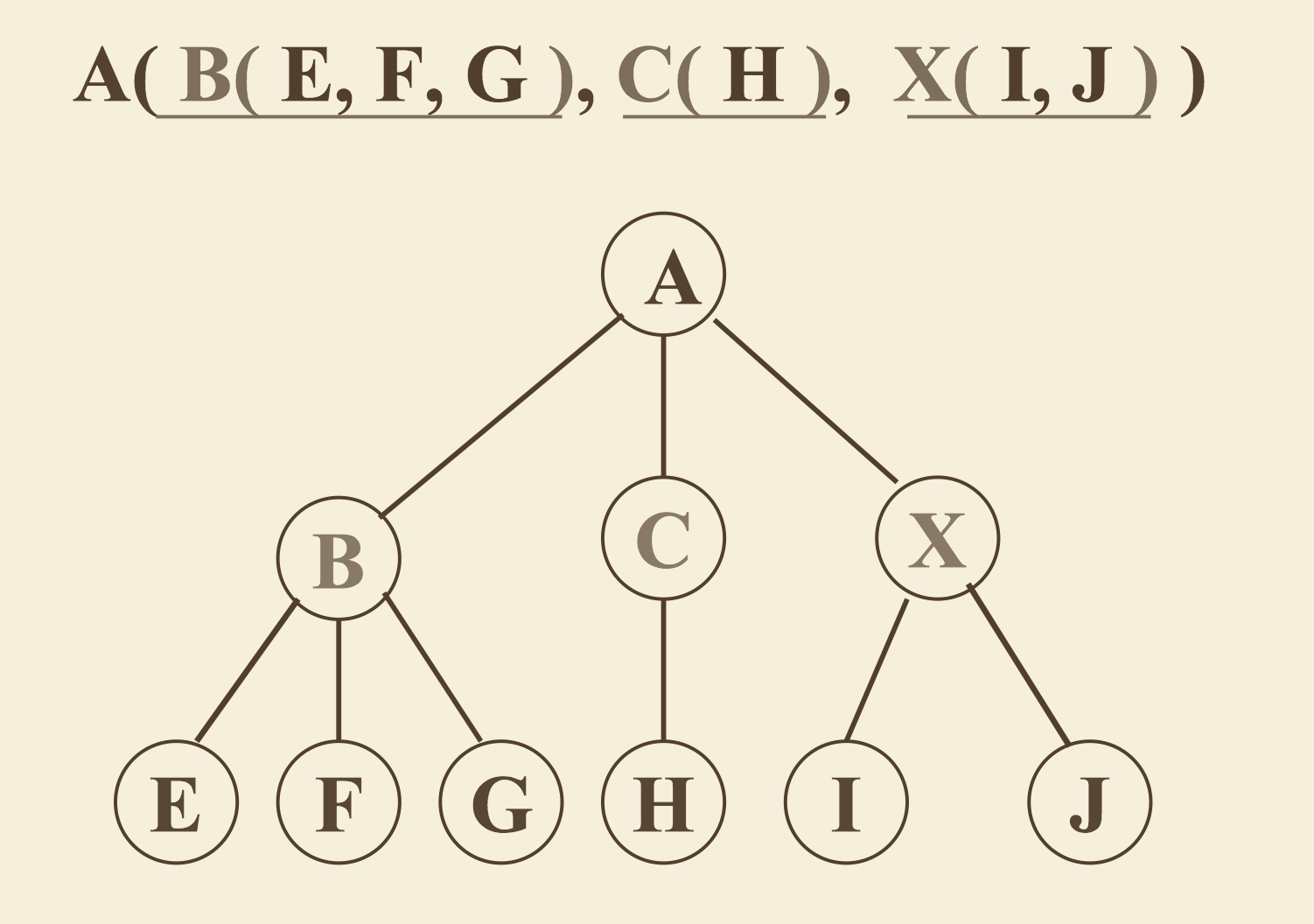
树形表示法：借助自然界中一棵倒置的树的形状来表示数据元素之间层次关系的方法。

1.4 树的基本名词术语

结点的度：该结点拥有的子树的数目。
树的度：树中结点度的最大值。
叶结点：度为 0 的结点。
分支结点: 度非 0 的结点。
层次的定义: 根结点为第一层，若某结点在第 i 层，则其孩子结点（若存在）为第 i+1 层。
树的深度: 树中结点所处的最大层次数。
树林(森林): $m \ge 0$ 棵不相交的树组成的树的集合。
树的有序性: 若树中结点的子树的相对位置不能随意改变，则称该树为有序树，否则称该树为无序树。

1.5 二叉树的定义

二叉树是 $n \ge 0$ 个结点的有穷集合 D 与 D 上关系的集合 R 构成的结构。当 $n = 0$ 时，称该二叉树为空二叉树；否则，它为包含了一个根结点以及两棵不相交的、分别称之为左子树与右子树的二叉树。

1.6 二叉树的基本形态

空、根、根 — 左子树、根 — 右子树、根 — 左子树 & 右子树。

2．完全二叉树与满二叉树的基本概念，二叉树的基本性质及其应用；

2.1 满全二叉树的定义

若一棵二叉树中的结点，或者为叶结点，或者具有两棵非空子树,并且叶结点都集中在二叉树的最下面一层。这样的二叉树为满二叉树。

2.2 完全二叉树的定义

若一棵二叉树中只有最下面两层的结点的度可以小于 2，并且最下面一层的结点（叶结点）都依次排列在该层从左至右的位置上。这样的二叉树为完全二叉树。

2.3 二叉树的基本性质

具有 n 个结点的非空二叉树共有 n–1 个分支。
- 除了根结点以外，每个结点有且仅有一个双亲结点，即每个结点与其双亲结点之间仅有一个分支存在，因此，具有n个结点的非空二叉树的分支总数为n–1。
非空二叉树的第 i 层最多有 $2^{i–1}$ 个结点（$i \ge 1$）。
- 当 $i = 1$ 时，结论显然正确。非空二叉树的第1层有且仅有一个结点，即树的根结点。
- 假设对于第 j 层（$1 \le j \le i–1$）结论也正确,即第 j 层最多有 $2^{j-1}$ 个结点。
- 由定义可知，二叉树中每个结点最多只能有两个孩子结点。若第 i–1 层的每个结点都有两棵非空子树,则第 i 层的结点数目达到最大。而第 i–1层最多有 $2^{i–2}$ 个结点已由假设证明，于是，应有 $2*2^{i-2} = 2^{i-1}$。
深度为 h 的非空二叉树最多有 $2^h-1$ 个结点。
- 由性质 2 可知，若深度为h的二叉树的每一层的结点数目都达到各自所在层的最大值,则二叉树的结点总数一定达到最大。即有 $2^0 + 2^1 + 2^2 + … +2^{i-1} + … + 2^{h-1} = 2^h-1$。
若非空二叉树有 $n_0$ 个叶结点，有 $n_2$ 个度为 2 的结点，则 $n_0 = n_2 + 1$。
- 设该二叉树有 $n_1$ 个度为 1 的结点，结点总数为 n，有 $n = n_0 + n_1 + n_2 $ -------- (1)
- 设二叉树的分支数目为 B,根据性质 1，有 $B = n-1$ -------- (2)
- 这些分支来自度于为 1 的结点与度为 2 结点，即 $B = n_1 +2n_2$ -------- (3)
- 联列关系(1)，(2)与(3)，可得到 $n_0 = n_2 + 1$。
- 推论：对于一般的树，有 $n_0 = n_2 + 2n_3 + 3n_{4} + ... + (m–1)n_{m} + 1$ 。
具有 n 个结点的非空完全二叉树的深度为 $h = \lfloor log_{2}n \rfloor + 1$。
若对具有 n 个结点的完全二叉树按照层次从上到下，每层从左到右的顺序进行编号，则编号为 i 的结点具有以下性质：
1. 当 $i = 1$，则编号为 i 的结点为二叉树的根结点；若 $i > 1$，则编号为 i 的结点的双亲的编号为 $ \lfloor i/2 \rfloor$；
2. 若 $2i > n$，则编号为 i 的结点无左子树；若 $2i \le n$，则编号为 i 的结点的左孩⼦的编号为 $2i$；
3. 若 $2i + 1 > n$，则编号为 i 的结点无右子树；若 $2i + 1 \le n$，则编号为 i 的结点的右孩子的编号为 $2i + 1$。

3．二叉树的顺序存储结构与二叉链表存储结构的基本原理；

3.1 二叉树的顺序存储结构

3.1.1 二叉树的顺序存储结构构造原理

根据完全二叉树的性质 6，对于深度为 h 的完全二叉树，将树中所有结点的数据信息按照编号的顺序依次存储到一维数组 $BT[0:2^h-2]$ 中，由于编号与数组下标一一对应，该数组就是该完全二叉树的顺序存储结构。

对于一般二叉树, 只须在二叉树中“添加”一些实际上二叉树中并不存在的“虚结点” ( 可以认为这些结点的数据信息为空)，使其在形式上成为一棵“完全二叉树”，然后按照完全二叉树的顺序存储结构的构造方法将所有结点的数据信息依次存放于数组 $BT[0: 2^h -2]$ 中。

3.2 二叉树的链表存储结构

3.2.1 二叉树的链表存储结构构造原理

链结点构造为：lchild | data | rchild
其中，data 为数据域；lchild 与 rchild 分别为指向左、右子树的指针域。

3.2.2 二叉树的链表存储结构定义

typedef int ElemType;
typedef struct Node {
    ElemType data;
    struct Node *lchild, *rchild;
}BTNode, *BTree;

3.2.3 广义表建立二叉树

BTree CREATE_BTREE() {
    BTree stack[MAXN], p, T = NULL;
    char ch;
    int flag, top = -1;
    while (1) {
        scanf("%c",&ch);
        switch (ch) {
            case '@':
                return T;
            case '(':
                stack[++top] = p;
                flag = 1;
                break;
            case ')':
                top--;
                break;
            case ',':
                flag = 2;
                break;
            default:
                p = (BTree)malloc(sizeof(BTNode));
                p->data = ch;
                p->lchild = NULL;
                p->rchild = NULL;
                if (T == NULL) {
                    T = p;
                } else if (flag == 1) {
                    stack[top]->lchild = p;
                } else if (flag == 2) {
                    stack[top]->rchild = p;
                }
                break;
        }
    }
}

3.2.4 求二叉树叶结点的数目

int LEAF_COUNT_BTREE(BTree T) {
    if (T == NULL) {
        return 0;
    }
    if (T->lchild == NULL && T->rchild == NULL) {
        return 1;
    }
    return LEAF_COUNT_BTREE(T->lchild) + LEAF_COUNT_BTREE(T->rchild);
}

3.2.5 求二叉树的深度

int DEPTH_BTREE(BTree T) {
    int leftDepth,rigthDepth;
    if (T == NULL) {
        return 0;
    } else {
        leftDepth = DEPTH_BTREE(T->lchild);
        rigthDepth = DEPTH_BTREE(T->rchild);
        if (leftDepth > rigthDepth) {
            return leftDepth + 1;
        } else {
            return rigthDepth + 1;
        }
    }
}

3.2.6 访问结点的数据域

void VISIT_NOTE_BTREE(BTree T) {
    if (T != NULL) {
        printf("%3c",T->data);
    }
}

4．二叉树的前序遍历、中序遍历、后序遍历和按层次遍历，重点是二叉树在以二叉链表作为存储结构基础上各种遍历算法（包括非递归算法）的设计与应用；

4.1 二叉树的前序遍历

若被遍历的二叉树非空, 则：
1. 访问根结点；
2. 以前序遍历原则遍历根结点的左子树；
3. 以前序遍历原则遍历根结点的右子树。

4.1.1 二叉树的前序遍历（递归算法）

void PRE_ORDER_TRAVERSE(BTree T) {
    if (T != NULL) {
        VISIT_NOTE_BTREE(T);
        PRE_ORDER_TRAVERSE(T->lchild);
        PRE_ORDER_TRAVERSE(T->rchild);
    }
}

4.1.2 二叉树的前序遍历（非递归算法）

算法步骤：

当 p 指向的结点不为空时，访问该结点，并将该结点入栈，再将 p 指向该结点的左孩子结点。
然后继续步骤 1，直到 p 指向的结点为空。
当 p 指向的结点为空时，且堆栈不为空时，从堆栈中退出栈顶元素（某个结点的地址）送 p，然后将 p 指向该结点的右孩子结点。
重复上边的步骤，直到 p 为空，并且堆栈也为空，遍历结束。

算法实现：

void PRE_ORDER(BTree T) {
    BTree stack[MAXN], p = T;
    int top = -1;
    if (T != NULL) {
        do {
            while (p != NULL) {
                VISIT_NOTE_BTREE(p);
                stack[++top] = p;
                p = p->lchild;
            }
            p = stack[top--];
            p = p->rchild;
        } while (p != NULL || top != -1);
    }
}

4.2 二叉树的中序遍历

若被遍历的二叉树非空, 则：
1. 以中序遍历原则遍历根结点的左子树；
2. 访问根结点；
3. 以中序遍历原则遍历根结点的右子树。

4.2.1 二叉树的中序遍历（递归算法）

void IN_ORDER_TRAVERSE(BTree T) {
    if (T != NULL) {
        IN_ORDER_TRAVERSE(T->lchild);
        VISIT_NOTE_BTREE(T);
        IN_ORDER_TRAVERSE(T->rchild);
    }
}

4.2.2 二叉树的中序遍历（非递归算法）

算法步骤：

当 p 指向的结点不为空时，并将该结点入栈，再将 p 指向该结点的左孩子结点。
然后继续步骤 1，直到 p 指向的结点为空。
当 p 指向的结点为空时，且堆栈不为空时，从堆栈中退出栈顶元素（某个结点的地址）送 p，并访问该结点，然后将 p 指向该结点的右孩子结点。
重复上边的步骤，直到 p 为空，并且堆栈也为空，遍历结束。

算法实现：

void IN_ORDER(BTree T) {
    BTree stack[MAXN], p = T;
    int top = -1;
    if (T != NULL) {
        do {
            while (p != NULL) {
                stack[++top] = p;
                p = p->lchild;
            }
            p = stack[top--];
            VISIT_NOTE_BTREE(p);
            p = p->rchild;
        } while (p != NULL || top != -1);
    }
}

4.3 二叉树的后序遍历

若被遍历的二叉树非空, 则：
1. 以后序遍历原则遍历根结点的左子树；
2. 以后序遍历原则遍历根结点的右子树；
3. 访问根结点。

4.3.1 二叉树的后序遍历（递归算法）

void POST_ORDER_TRAVERSE(BTree T) {
    if (T != NULL) {
        POST_ORDER_TRAVERSE(T->lchild);
        POST_ORDER_TRAVERSE(T->rchild);
        VISIT_NOTE_BTREE(T);
    }
}

4.3.2 二叉树的后序遍历（非递归算法）

对二叉树进行后序遍历的过程中，当指针 p 指向某一个结点时，不能马上对其进行访问，而要先遍历其左子树，因而要将节点进栈。
当其左子树遍历完之后，再次搜索到该结点时（通过退栈得到该结点地址），还不能对其进行访问，还要遍历它的右子树。所以，再一次将该结点入栈。
只有当该结点的右子树也遍历完之后，回到该结点，才能访问该结点。
所以，这里额外引入了一个栈 stack2[]，stack2[] 中存放标志位 flag，flag 用来表示当前结点是否可以被访问。
第一次将该结点入栈的时候，将标志位置为 0，第一次退栈的时候，判断标志位为 0，表示暂不访问（因为右子树尚未遍历）。
第二次将该结点入栈的时候，将标志位置为 1，第二次退栈的时候，判断标志位为 1，表示可以访问（此时右子树已经遍历）。

算法步骤：

当 p 指向的结点不为空时，并将该结点入栈，标志位 flag = 0 入栈，再将 p 指向该结点的左孩子结点。
然后继续步骤 1，直到 p 指向的结点为空。
当 p 指向的结点为空时，且堆栈不为空时，从堆栈 stack[]中退出栈顶元素（某个结点的地址）送 p。并从 stack1[]中取出标志位。
1. 如果 flag == 0，表示该结点右子树还未遍历，暂不访问，将 p 指向的结点再次进栈，并且将标志位 flag = 1 入栈，然后将 p 指向该结点的右孩子结点，重复上边的步骤。
2. 如果 flag == 1，表示该结点右子树已经遍历，可以访问，访问该结点，并将 p 指向空（因为该结点的左右子树都已经遍历完），重复上边的步骤。
重复上边的步骤，直到 p 为空，并且堆栈也为空，遍历结束。

算法实现：

void POST_ORDER(BTree T) {
    BTree stack[MAXN], p = T;
    int stack1[MAXN],flag,top = -1;
    while (T != NULL) {
        do {
            while (p != NULL) {
                stack[++top] = p;
                stack[top] = 0;
                p = p->lchild;
            }
            p = stack[top];
            flag = stack1[top--];
            if (flag == 0) {
                stack[++top] = p;
                stack1[top] = 1;
                p = p->rchild;
            } else {
                VISIT_NOTE_BTREE(p);
                p = NULL;
            }
        } while (p != NULL || top != -1);
    }
}

4.4 二叉树的层次遍历

若被遍历的二叉树非空, 则：
1. 按照层次从上到下，每一层从左到右依次访问结点。

4.4.1 二叉树的层次遍历（非递归算法）

void LAYER_ORDER(BTree T) {
    BTree queue[MAXN],p = T;
    int front,rear;
    front = 0;
    rear = 0;
    if (T != NULL) {
        queue[rear] = T;
        rear = (rear + 1) % MAXN;
        while (front < rear) {
            p = queue[front];
            front = (front + 1) % MAXN;
            VISIT_NOTE_BTREE(p);
            if (p->lchild != NULL) {
                queue[rear] = p->lchild;
                rear = (rear + 1) % MAXN;
            }
            if (p->rchild != NULL) {
                queue[rear] = p->rchild;
                rear = (rear + 1) % MAXN;
            }
        }
    }
    printf("\n");
}

4.5 由前序序列和中序序列恢复二叉树

BTree CREAT_BTREE_FROM_PRE_AND_IN_ORDER(char *preOrder, char *inOrder,int n) {
    if (n == 0) {
        return NULL;
    }
    int k = 0;
    while (preOrder[0] != inOrder[k]) {
        k++;
    }
    BTree T = (BTree)malloc(sizeof(BTNode));
    if (T != NULL) {
        T->data = inOrder[k];
        T->lchild = CREAT_BTREE_FROM_PRE_AND_IN_ORDER(preOrder+1, inOrder, k);
        T->rchild = CREAT_BTREE_FROM_PRE_AND_IN_ORDER(preOrder+k+1, inOrder+k+1, n-k-1);
        return T;
    } else {
        return NULL;
    }
}

4.6 由中序序列和后序序列恢复二叉树

BTree CREAT_BTREE_FROM_IN_AND_POST_ORDER(char *inOrder, char *postOrder, int n) {
    if (n == 0) {
        return NULL;
    }
    int k = 0;
    while (postOrder[n-1] != inOrder[k]) {
        k++;
    }
    BTree T = (BTree)malloc(sizeof(BTNode));
    if (T != NULL) {
        T->data = inOrder[k];
        T->rchild = CREAT_BTREE_FROM_IN_AND_POST_ORDER(inOrder+k+1, postOrder+k, n-k-1);
        T->lchild = CREAT_BTREE_FROM_IN_AND_POST_ORDER(inOrder, postOrder, k);
        return T;
    }
    return NULL;
}

5．二叉排序树的基本概念、建立（插入）、查找以及平均查找长度ASL的计算。

5.1 二叉排序树的基本概念

二叉排序树或者为空二叉树, 或者为具有以下性质的二叉树：

若根结点的左子树不空, 则左子树上所有结点的值都小于根结点的值；
若根结点的右子树不空, 则右子树上所有结点的值都大于或者等于根结点的值；
每一棵子树分别也是二叉排序树。

5.2 二叉排序树的建立

设 $K = ( k_1，k_2，k_3， … ，k_n )$ 为具有 n 个数据元素的序列。从序列的第一个元素开始，依次取序列中的元素，每取一个元素 $k_i$，按照下述原则将 $k_i$ 插入到二叉树中：

若二叉树为空, 则 $k_i$ 作为该二叉树的根结点；
若二叉树非空, 则将 $k_i$ 与该二叉树的根结点的值进行比较, 若 $k_i$ 小于根结点的值，则将 $k_i$ 插入到根结点的左子树中；否则，将 $k_i$ 插入到根结点的右子树中。

将 $k_i$ 插入到左子树或者右子树中仍然遵循上述原则。

5.2.1 二叉树的建立（插入）（递归算法）

void INSERT_SBTREE(SBTree &T, ElemType item) {
    if (T == NULL) {
        T = (SBTree)malloc(sizeof(SBTNode));
        T->data = item;
        T->lchild = NULL;
        T->rchild = NULL;
    } else if (item < T->data) {
        INSERT_SBTREE(T->lchild, item);
    } else {
        INSERT_SBTREE(T->rchild, item);
    }
}

5.2.2 二叉树的建立（插入）（非递归算法）

void INSERT_LINK_SBTREE(SBTree &T, ElemType item) {
    SBTree p = (SBTree)malloc(sizeof(SBTNode));
    p->data = item;
    p->lchild = NULL;
    p->rchild = NULL;
    if (T == NULL) {
        T = p;
    } else {
        SBTree q = T;
        while (1) {
            if (item < q->data) {
                if (q->lchild != NULL) {
                    q = q->lchild;
                } else {
                    q->lchild = p;
                    break;
                }
            } else {
                if (q->rchild != NULL) {
                    q = q->rchild;
                } else {
                    q->rchild = p;
                    break;
                }
            }
        }
    }
}

5.2.1 二叉排序树的建立（插入）主方法

SBTree CREAT_SBTREE(ElemType k[], int n) {
    SBTree T = NULL;
    for (int i = 0; i < n; i++) {
        INSERT_LINK_SBTREE(T, k[i]);
    }
    return T;
}

5.3 二叉排序树的查找

查找过程：

若二叉排序树为空，则查找失败，结束。
若二叉排序树非空，则将被查找元素与二叉排序树的根结点的值进行比较。
1. 若等于根结点的值,则查找成功，返回被查到元素所在链结点的地址，查找结束；
2. 若小于根结点的值,则到根结点的左子树中重复上述查找过程；
3. 若大于根结点的值,则到根结点的右子树中重复上述查找过程。
直到查找成功或者失败。

5.3.1 二叉排序树的查找（递归算法）

SBTree Search_SBTREE2(SBTree T, ElemType item) {
    if (T == NULL) {
        return NULL;
    }
    if (item == T->data) {
        return T;
    } else if (item < T->data) {
        return Search_SBTREE2(T->lchild, item);
    } else {
        return Search_SBTREE2(T->rchild, item);
    }
}

5.3.2 二叉排序树的查找（非递归算法）

SBTree SEARCH_SBTREE(SBTree T, ElemType item) {
    SBTree p = T;
    while (p != NULL) {
        if (item == p->data) {
            break;
        } else if (item < p->data) {
            p = p->lchild;
        } else {
            p = p->rchild;
        }
    }
    return p;
}

5.3.3 二叉排序树的平均查找长度 ASL

内路径长度（IPL）：从二叉树根结点到某结点所经过的分支数目定义为该结点的路径长度。二叉树中所有结点的路径长度之和定义为该二叉树的内路径长度。
外路径长度（EPL）：为了分析查找失败时的查找长度，在二叉树中出现子树时，增加新的空叶结点来代表这些空子树，从而得到一棵扩充后的二叉树。为了与扩充前的二叉树相区别，这些新增添的空的叶结点用小方块代表，称之为外部结点，树中原有的结点称为内部结点。扩充后的二叉树中所有外部结点的路径长度之和定义为该二叉树的外路径长度。根据二叉树的性质，若扩充后的二叉树有 n 个内部结点，必然有 n+1 个外部结点。
- $EPL = IPL + 2n$
平均查找长度（ASL）：确定一个元素在树中位置所需要进行的比较次数的期望值。
- 查找成功平均查找长度（ASL）：在 n 个结点的二叉排序树中，若对每个数据的查找概率相等，则对每个结点查找成功所需的比较次数就是该结点所在的层次数，即等于该结点的路径长度加 1。 $ASL = {IPL + n \over n}$
- 查找失败平均查找长度（ASL）：比较次数等于表示该数据元素所在范围的外部结点的路径长度。 $ASL = {EPL \over n+1} = {IPL+2n \over n+1}$
- 平均查找长度（ASL）：考虑到在二叉排序树中查找成功与不成功的全部可能性，设对扩充后的二叉树的每个结点（包括内部结点和外部结点）进行查找的概率相等，则平均查找长度为： $ASL = {IPL + n + EPL \over n + n + 1 } = {2IPL + 3n \over 2n + 1}$

例题：根据下图求出 IPL、EPL、ASL。

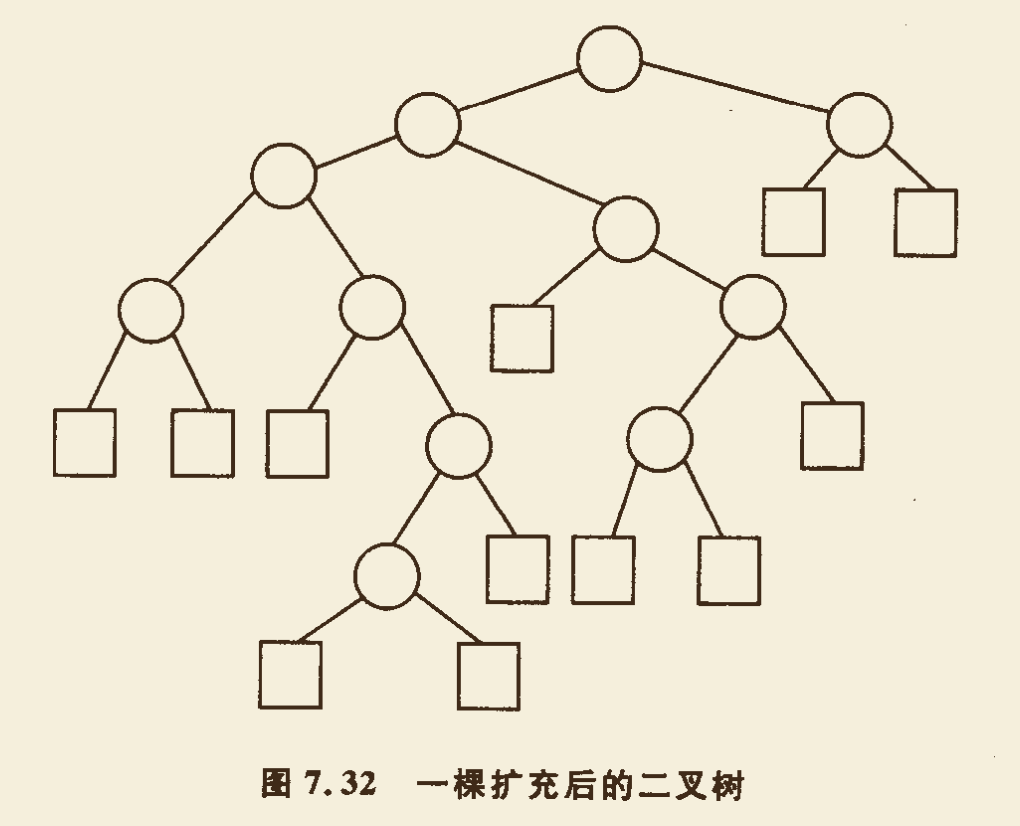
图中所示二叉树内路径长度（IPL）、外路径长度（EPL）和平均查找长度（ASL）如下：

$IPL = 1 * 2 + 2 * 2 + 3 *3 + 4 * 2 + 5 * 1 = 28$

$EPL = 2*2 + 3*1 + 4*4 + 5*3 + 6*2 = 50$

$ASL = {2*28 + 3*11 \over 2*11+1} = {89 \over 23}$

赏

本文作者： 程序员充电站
本文链接： https://itcharge.cn/life/graduate-test/buaa-data-structure-summary-05-tree-binarytree/
版权声明： 本站所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。

1．树与二叉树的基本概念，基本特征、名词术语；

1.1 树的定义

1.2 树的基本特征

1.3 树的逻辑表示方法

1.4 树的基本名词术语

1.5 二叉树的定义

1.6 二叉树的基本形态

2．完全二叉树与满二叉树的基本概念，二叉树的基本性质及其应用；

2.1 满全二叉树的定义

2.2 完全二叉树的定义

2.3 二叉树的基本性质

3．二叉树的顺序存储结构与二叉链表存储结构的基本原理；

3.1 二叉树的顺序存储结构

3.1.1 二叉树的顺序存储结构构造原理

3.2 二叉树的链表存储结构

3.2.1 二叉树的链表存储结构构造原理

3.2.2 二叉树的链表存储结构定义

3.2.3 广义表建立二叉树

3.2.4 求二叉树叶结点的数目

3.2.5 求二叉树的深度

3.2.6 访问结点的数据域

4．二叉树的前序遍历、中序遍历、后序遍历和按层次遍历，重点是二叉树在以二叉链表作为存储结构基础上各种遍历算法（包括非递归算法）的设计与应用；

4.1 二叉树的前序遍历

4.1.1 二叉树的前序遍历（递归算法）

4.1.2 二叉树的前序遍历（非递归算法）

4.2 二叉树的中序遍历

4.2.1 二叉树的中序遍历（递归算法）

4.2.2 二叉树的中序遍历（非递归算法）

4.3 二叉树的后序遍历

4.3.1 二叉树的后序遍历（递归算法）

4.3.2 二叉树的后序遍历（非递归算法）

4.4 二叉树的层次遍历

4.4.1 二叉树的层次遍历（非递归算法）

4.5 由前序序列和中序序列恢复二叉树

4.6 由中序序列和后序序列恢复二叉树

5．二叉排序树的基本概念、建立（插入）、查找以及平均查找长度ASL的计算。

5.1 二叉排序树的基本概念

5.2 二叉排序树的建立

5.2.1 二叉树的建立（插入）（递归算法）

5.2.2 二叉树的建立（插入）（非递归算法）

5.2.1 二叉排序树的建立（插入）主方法

5.3 二叉排序树的查找

5.3.1 二叉排序树的查找（递归算法）

5.3.2 二叉排序树的查找（非递归算法）

5.3.3 二叉排序树的平均查找长度 ASL

最新文章

热门标签

联系方式

目 录

目录